Executive Summary

By combining existing qubit technology, our proprietary quantum networking technology, and the latest thinking on quantum error correction (QEC) adapted to distributed architectures, we propose the first (to our knowledge) viable blueprint for building large fault tolerant quantum computers.

• We apply error correction higher in QC stack than with monolithic QC models, mediated by a distributed quantum-network; ‘Dist-QEC’. Local quantum error correction proposals cannot improve the logical qubit lifetime without redesigning the node. Through distributed QEC, our systems can improve in capacity and lifetime through horizontal scaling.
• Distributed quantum error correction is enabled by and demands low latency distributed control that we offer through our position as integrator.
• Some promising, novel error correction codes are accessible only with long-range photonic networking such as the ones that we are developing, including high rate topological codes that can be co-designed with the quantum hardware.
• We have developed a code design methodology and error model that allows flexing of relevant parameters in the exploitation of these codes, with the prediction of finding ‘Goldilocks’ points (e.g. quality vs scale) that can give a path to a most efficient and realisable design.
• Early indications are that a ‘Blueprint’ can be derived, allowing the construction of a system delivering an arbitrary number of logical qubits from the linear scaling of system components such as ‘QPUs’ and QNUs’.
• The model indicates near-term achievable (3~4 years) metrics for these components both in terms of quality (fidelity) and scale
  • ~99.99% local fidelity
  • ~99.5% non-local fidelity
  • <<50 qubits per QPU minimum
• There are indications that these codes offer fast logical clifford gates, easing the implementation of fault tolerant algorithms.

Nu Quantum’s Error Model

Nu Quantum have built an error model which characterises the errors from both ‘local’ on chip qubit error, and error from ‘non-local’ imperfect extra-device entanglement generation our error model estimates the effect of qubit decoherence, qubit measurement errors and imperfect photonic entanglement generation. The model considers the following local errors:

• General depolarising noise applied to all qubits due to decoherence (99.99%);
• Measurement errors during syndrome extraction;
• State preparation and reset errors.

However, to model a modular network design we also consider:

• Fidelity of the Bell pair generation scheme, which may differ from the local noise levels (99.5%);
• Increased qubit (ancilla) overhead required to generate non-local Bell pairs;
• Additional decoherence observed due to wait-time while generating non-local entanglement (30 gate-cycles).

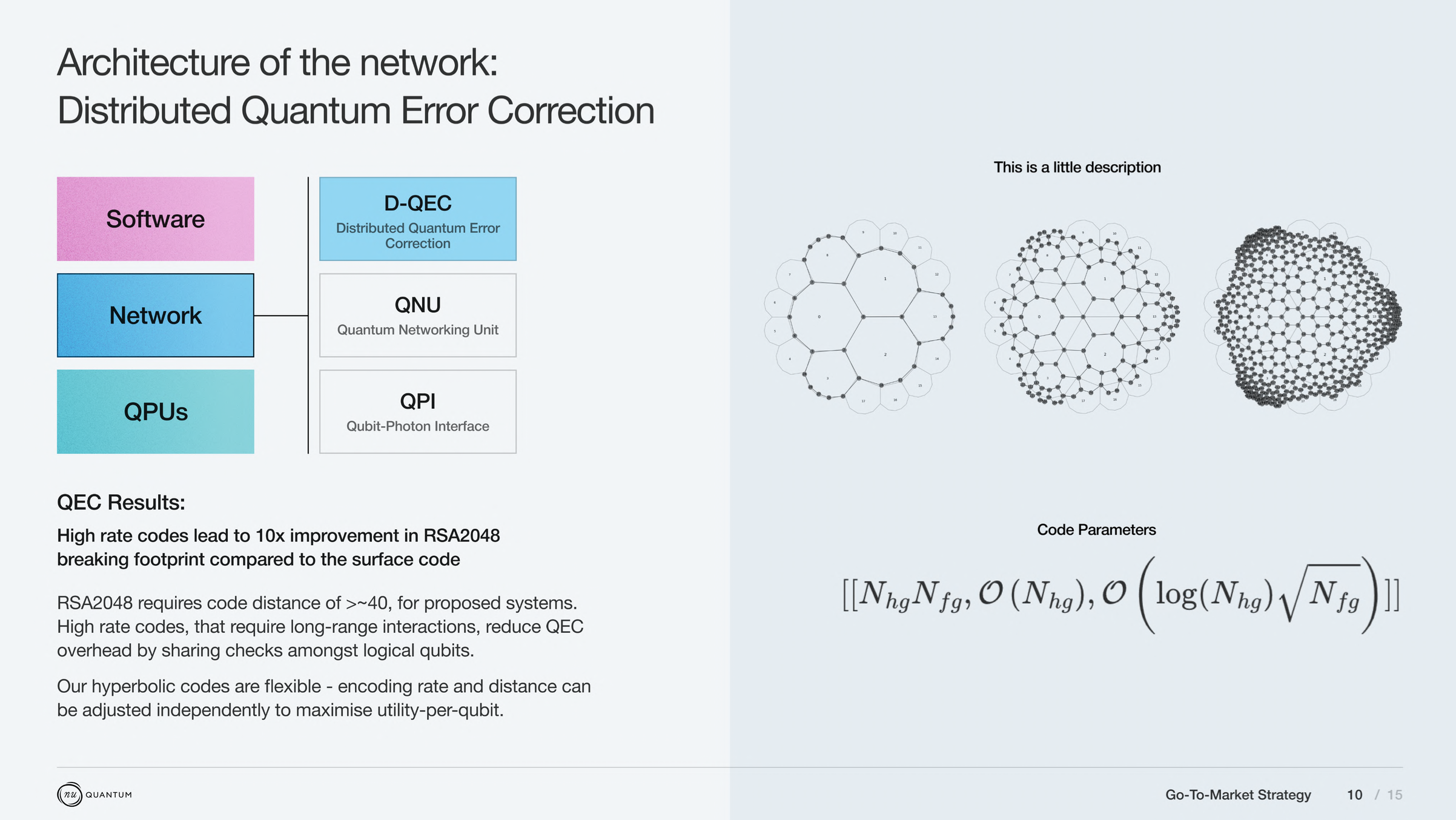
High Genus Codes

We have identified new codes which…

• Have a high encoding ratio, providing many logical qubits per physical qubit and node;
• Are directly realisable on distributed quantum systems;
• Have practical error thresholds (fidelity) that vary from approximately 99.2% non-local and 99.9% local under our current error model, improving depending on the “fine graining” level. When operations are performed with a fidelity above the threshold, error correction will exponentially suppress any errors.
• All code instances require the same QPU and QNU building blocks, in varying quantities. This allows us substantial flexibility to pick a goldilocks code tailored to QPU performance and varying circuit width or depth targets with the same building blocks. And the capability to expand the system by gradual installation of QPUs.

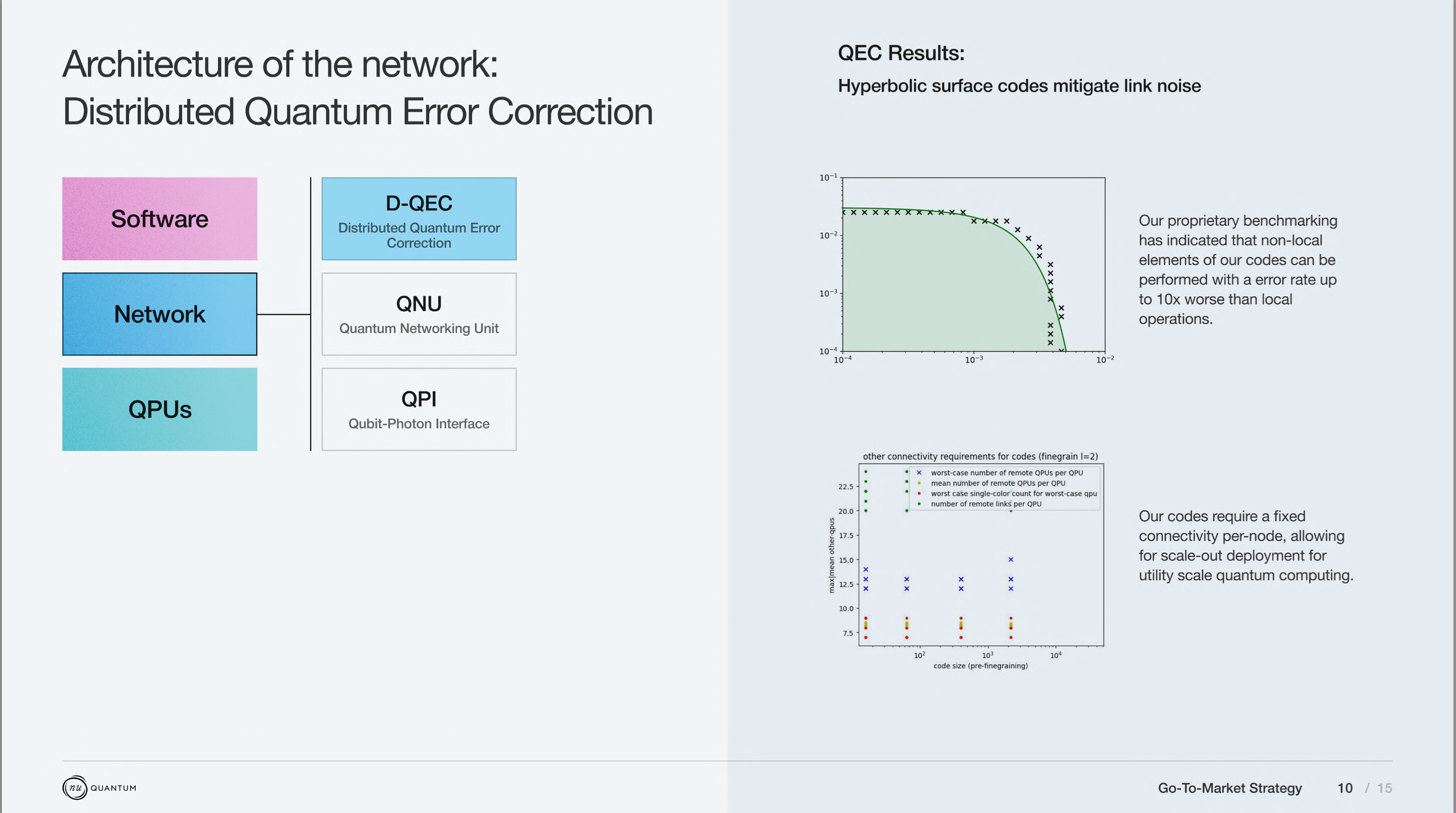
Connectivity requirements,

• Each device in the distributed architecture has a static connectivity requirement over the lifetime of the code. To operate, a device only needs to be able to generate a shared Bell pair with a small, fixed number of other devices. The optical switches can be a fixed depth that does not vary with system size or the number of QPUs.

Advantages and disadvantages over surface code and LDPC codes.

• Distributed error correction techniques can provide more logical capacity at a given cost by enabling efficient error correction on devices of manufacturable scale. These high rate codes are only possible on distributed systems or on bi-layer architectures, which do not exist today.
• Our design is feasible from 10’s of qubits per node, requiring no breakthroughs in qubit density or fidelity to achieve industrially relevant scale. The benefits of a distributed architecture achieve utility with fewer physical qubits than a monolithic surface code, and is feasible within current ion trap qubit technology.
• Within our chosen code family, we believe we will have access to the full Clifford group of fault tolerant operations. This is through a combination of using sequences of low-weight measurements that can be incorporated into an standard error correction code cycle, and implementing non-local operations by taking advantage of the flexible connectivity provided by photonic switching. This is expected to improve our Clifford gate performance over both 2d surface codes using lattice surgery, and qLDPC codes using 2d surface codes for logical operations. Additionally, as we do not pay routing costs for moving logical qubits, we can also use algorithms optimized for qubit footprint rather than routing overhead, further reducing the logical error rate target required for useful operation.